반응형
트리(Tree)
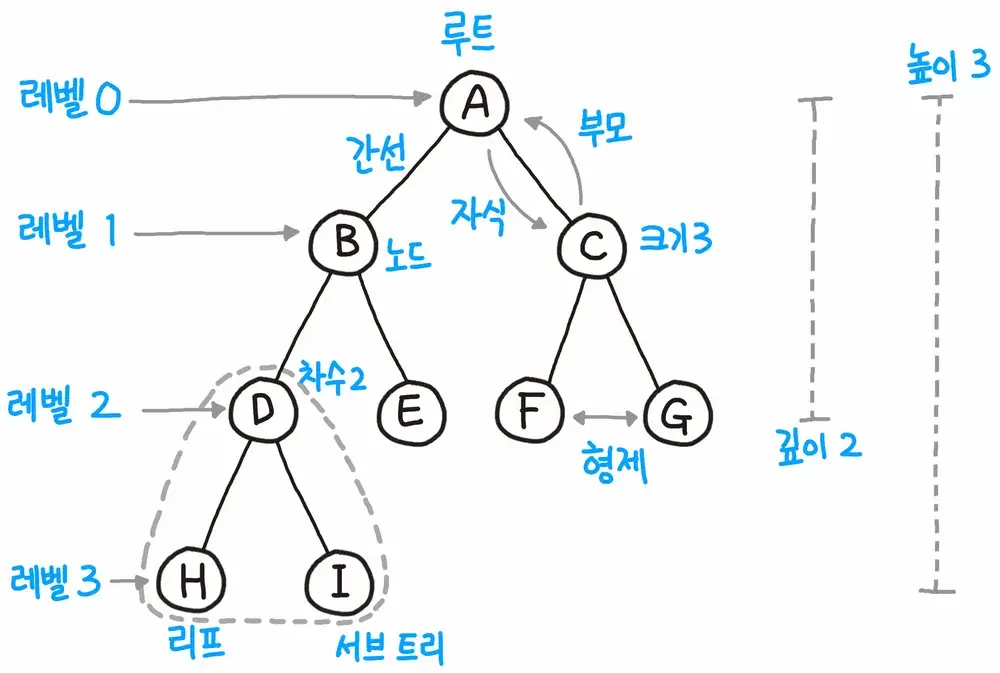
- 노드와 엣지로 연결된 그래프의 특수한 형태 -> 그래프의 일종
- 순환구조(cycle)를 가지고 있지 않고, 1개의 루트 노드 존재
- 루트 노드 제외 모두 단하나의 부모 노드 존재
- 연결된 트리의 경우 임의의 두 노드를 연결하는 경로는 유일
- 트리도 그래프의 일종이기에 그래프로 풀이 가능 -> 인접리스트로 표현(dfs, bfs)
- 트리만을 위한 문제 -> 이진트리, 인덱스트리, LCA(최소공통조상)
이진트리(Binary Tree)
- 각 노드의 자식 노드 개수(=차수)가 2 이하로 구성된 트리
- 일차원배열로 표한하기 위해서는 무조건 이진트리
- 포화이진트리 : 리프 노드가 모두 차있는 상태
- 완전이진트리 : 마지막 레벨은 왼쪽부터 채워져 있는 상태
- 왼쪽 자식 노드 = 현재 index*2
- 오른쪽 자식 노드 = 현재 index*2 + 1

인덱스 트리(Index Tree) = 세그먼트 트리
- 구간합과 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조
- 구간합의 경우 기존의 합배열로도 가능 -> But, 데이터의 업데이트가 느림
※ 합배열 : 일차원배열을 생성해 리프노드를 먼저 채우고, 인덱스/2를 통해 부모 노드에 합을 저장하는 방식 - 구간합, 최대/최소 구하기에 사용
단계
1. 트리 초기화하기
리프 노드만 원본 데이터이고, 그의 부모 노드들을 업데이트 한다. 트리 배열의 크기의 경우 2^k>=N 을 만족시키는 최소 k를 찾은 후 2^k * 2를 트리 배열 크기로 정의한다. 2^k를 리프 시작 노드로 잡고 데이터를 넣는다.
2. 구간합 A[N] = A[2N] + A[2N+1], 최대 A[N] = max(A[2N], A[2N+1]), 최소 A[N] = min((A[2N], A[2N+1])
3. 질의값 구하기
우선 질의 인덱스를 인덱스 트리의 리프 노드에 해당하는 인덱스로 변경한다. 주어진 질의 index + 2^k -1 로 변경한다. 변경한 start index가 2로 나누었을 때 나머지가 1이면 이는 해당 노드가 자식 노드의 오른쪽 위치에 있다는 것이기 때문에 부모 노드를 더하지 않기 위해 추가로 더해줄 노드로 별도로 선택하고, end index가 2로 나누었을 때 나머지가 0이라면 이는 해당 노드가 자식노드의 왼쪽 위치에 있다는 것이기 때문에 부모 노드를 더하지 않기 위해 추가로 더해줄 노드로 별도로 선택한다. 이후 start = (start+1)/2, end = (end-1)/2로 start와 end index를 부모 노드로 이동시키면서 해당 과정을 반복하고, start > end일 때까지 위 과정을 반복한다.
4. 업데이트
이진 트리에서 부모 노드로 가는 방식으로 /2를 진행하며 값을 업데이트 한다.
LCA(최소 공통 조상)
- 트리 그래프에서 임의의 두 노드를 선택했을 때 두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드
일반적으로 찾는 방법
- 트리 높이가 크지 않을 때 = 시간 제한이 타이트하지 않을 때
- 루트 노드에서 시작해 각 노드의 부모 노드와 깊이를 저장
- DFS, BFS를 이용해 수행
- 두 노드의 깊이가 다를 경우 하나를 다른 하나의 깊이만큼 올라오게 만든 후 부모 노드를 계속 탐색
빠르게 찾는 방법
- 깊이를 맞춰 주거나 같아지는 노드를 찾을 때 기존 한단계씩 올라가던 방법에서 2^k 씩 올라가면서 비교
- 자신의 부모 노드만 저장해 놓던 방식에서 2^k 번째 위치의 부모 노드까지 저장
- 부모 노드 저장 배열 만들기 -> 2차원 배열
P[K][N] = N번 노드의 2^K 번의 부모 노드 번호 - P[K][N] = P[K-1][P[K-1][N]]
- P[2][6] = 6번 노드의 2^2 번의 부모 노드 번호
- P[1][P[1][6]] = 6번 노드의 2^1번의 부모 노드 번호의 2^1번의 부모 노드 번호
반응형
'코테 준비 > Baekjoon Algorithm' 카테고리의 다른 글
| [Day05 - 2750번] 수 정렬하기 (0) | 2024.02.13 |
|---|---|
| [Day05 - 이론] 버블 정렬 & 선택 정렬 (0) | 2024.02.13 |
| [백준(BOJ)] 10828번 C++ 풀이 (0) | 2022.02.27 |
| [백준(BOJ)] 2750번 C++ 풀이 (0) | 2021.11.24 |
| [백준(BOJ)] 2447번 C++ 풀이 (0) | 2021.08.03 |